Network meta-analysis is tailored to deal with multicomponent interventions such as self-management interventions. We briefly discuss the challenges of analyzing multicomponent interventions and the benefits and limitations of two approaches (standard network meta-analysis and component network meta-analysis).
Standard network meta-analysis (NMA) focuses on assessing combination of components whereas component network meta-analysis (CNMA) focuses on estimating component effects and then proceeds to reconstruct the effects of self-management interventions (SMIs) based on the component effects. But how to explore what self-management characteristics work (or do not work)?
The aim of COMPAR-EU is to compare the effectiveness of SMIs in four chronic diseases. With hundreds of randomized controlled trials and a plethora of different SMIs available, NMA is the appropriate method for this aim. SMIs are not easy to define as they consist of multiple, possibly interacting components. These components are not limited just to what is the SMI (sharing information, skills training etc.) but also include the mode of delivery (e.g. face-to-face vs. remotely), the provider (physician, nurse, etc.), the location (primary care, hospital, etc.), the type of encounter (clinical visits, self-guided, etc.) and the time of communication (synchronous vs. asynchronous). Additionally, there may be variations in other characteristics (e.g. duration, intensity). One can easily see that heterogeneity of SMI may be an issue.
Methodological vehicles (NMA and CNMA)
At the synthesis level, there are two main approaches for handling such interventions:
- Standard NMA, where each combination of components forms a distinct intervention.
- Component NMA, that estimates the effect of each component and then estimates the effect of a SMI by summing the effects of the components comprising this SMI (additivity assumption).
The former will answer the question ‘which SMI work’ whereas the latter will answer the question ‘which components work’.
Evidence Base
In COMPAR-EU, we have identified 43 distinct characteristics (components) of SMIs and, after long discussions, grouped them down to 13 (plus two versions of a usual care). Ideally, we would like to estimate the effect of each of the 43 components, but we had to proceed to some clinically meaningful merging to avoid ending up with each study comparing different SMIs. There is a cost to that, information is lost by merging characteristics and this may lead to a substantial increase in heterogeneity. Subsequently, NMA assumptions such as transitivity (the ability to estimate effects indirectly) may be challenged.
To understand the challenges in the analysis with SMIs, even with a considerable merging of components, have a look at the network plot below (the outcome is all-cause hospital admissions, nodes/circles represents SMIs and edges/lines represent studies comparing the connected SMIs). There is a total of 60 studies. A meta-analyst would normally be delighted with this number. But these 60 studies compare 33 different SMIs (combination of different SMI components)!
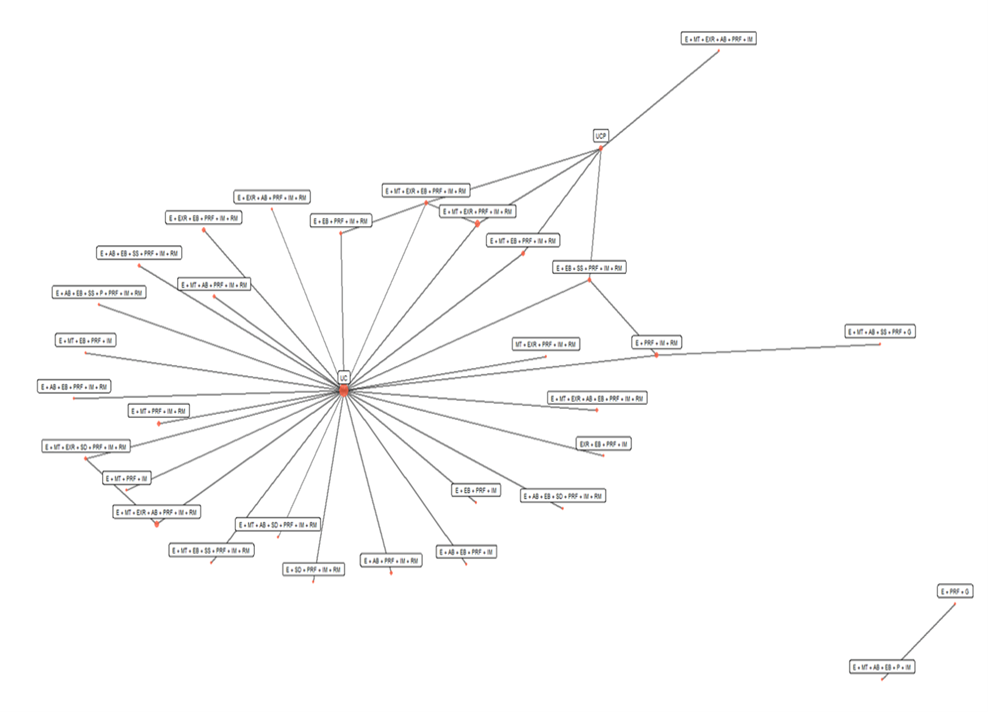
We have observed similar patterns in all outcomes (more than 80) we have analyzed. More specifically:
- Networks are sparse. Most SMIs are compared to usual care (UC) and not to each other. In this outcome, 52 of the 60 trials (87%) compare a SMI to UC.
- For most comparisons (528 in this network!), information comes either only from direct evidence (studies directly comparing the SMIs of the comparison – lines in the network plot) or from indirect evidence (two SMIs not compared in any trial – no line in the network plot).
- Studies are small and associated with much uncertainty. The relative effect of each SMI vs UC is informed mainly by the study including this comparison. We may end up with a SMI with a large effect in the NMA just because this SMI is compared in a single trial at high risk of bias. This has also implications for the main NMA assumptions (agreement between direct and indirect evidence).
- There is substantial heterogeneity of the SMI effect.
- In all outcomes there are studies not connected to the main network (in this outcome there is only one).

Dr Dimitris Mavridis
Dimitris has been involved in evidence synthesis for a decade now. He acts as a reviewer both for the Cochrane and the Campbell collaborations. He also serves as an associate editor for ‘Research Synthesis Methods’ and the series ‘statistics in practice’ in the ‘Evidence Based Mental Health’ journal. He has published many NMA and has been working mainly on statistical methodology surrounding NMA.
Interpretation of results
Apart from all these, interpretation of results is not straightforward. Partly due to imprecision in results and partly due to the fact that there is not a clear pattern between effect sizes and presence/absence of components in SMIs. Consider the table below. What are the conclusions? Adding component D worsens the outcome but adding both components D and E improves the outcome? It is tempting (and wrong) to focus on point estimates and statistical significance. The 95% CIs are huge and all the information comes from the small trials including these interventions. Hence, we additionally need to consider imprecision, the risk of bias and quality of these studies when interpreting the results. In this network, we have 30 relative effects of SMIs vs. UC and interpretation is much more complicated.

Component network meta-analysis attempts to solve some of these issues. The effect of a combination of components equals the sum of the effects of its components e.g.
![]()
This is known as the additivity assumption. Instead of estimating the effect of A+B+C from the couple trials comparing this SMI, you estimate it through the effects of its components, which are included in many trials each. As a result, we have
- more precise effect estimates
- effects closer to the null. Since components are included in trials with both small and large effects, when combining them to get the effect of the SMI, it is unlikely to see very large effects like those observed in standard NMA.
CNMA may give us information on which components are not working. A component included in SMIs with small effects is expected to have a negative impact on the SMIs in general. It also includes studies not connected to the main network, because all studies are connected at the component level.
Remaining challenges
Suppose now that the CNMA concludes that components A, B and C are effective, but these have never been combined in any of the trial arms. Is it rational to suggest a SMI with these components? Some content knowledge is probably useful. Additionally, the additivity assumption of CNMA is a hard one to defend. In practice, complex interventions such as SMIs are full of interdependencies (interactions) and non-linear responses. An interaction effect occurs when the effect of one component depends on the value of another component. We can express it like this
![]()
The interaction term can be positive (the two components act synergistically), negative (antagonistically) or zero (independently). The possible combinations of components are innumerable and we cannot just add interactions everywhere. Ideally, we would like content knowledge on where (which components) to add interaction terms. This is not an easy task, and ignoring interaction terms challenges the interpretation of the component effects.
So how are we supposed to analyze such a network? Albert Einstein said that if you have an hour to solve a problem, you should spend 55 minutes thinking about the problem and 5 minutes thinking about the solution. We have been thinking about the problem for some months now, trying to formulate the right questions, and according to my calculations we can afford going on like this for some extra months. But at some point we have to enter the five minute period of solving the problem. Yet, with such a complex dataset, with multiple components, outcomes and analyses, there is a high likelihood we will find patterns in the noise. Finding meaningful and important patterns in the data is the main challenge. To this end, we will try not even NMA and CNMA but a series of regression analyses and visual tools to understand interdependencies between components, with an aim to find SMI characteristics and their combinations that work, but also those that do not.




